Basics
Contents
Layer is a building block for constructible neural networks. NeuPy has a simple and flexible framework that allows to construct complex neural networks easily.
Join layers
Let’s start with basics. The most useful function to define relations between layers is layers.join. It accepts sequence of layers and joins them into the network.
>>> from neupy.layers import *
>>>
>>> join(Sigmoid(1), Sigmoid(2))
<unknown> -> [... 2 layers ...] -> (?, 2)
>>>
>>> join(Sigmoid(2), Sigmoid(1))
<unknown> -> [... 2 layers ...] -> (?, 1)
Inline operator
Also, NeuPy provides a special inline operator that helps to define sequential relations between layers.
>>> from neupy.layers import *
>>> Sigmoid(2) >> Sigmoid(1)
<unknown> -> [... 2 layers ...] -> (?, 1)
Code above does exactly the same as join(Sigmoid(2), Sigmoid(1)).
Input layer
In the network, shape of the expected input has to be specified explicitly. It’s possible to define expected input shape using the Input layer.
>>> from neupy.layers import *
>>> Input(3) >> Sigmoid(2) >> Sigmoid(1)
(?, 3) -> [... 3 layers ...] -> (?, 1)
The Input layer expects features shape of each individual sample passed through the network as a first argument. In the example above, we say that each input sample will have 3-dimensional features.
Multi-dimensional inputs can be specified as a tuple.
>>> Input((28, 28, 1)) >> Convolution((3, 3, 16)) >> Relu()
(?, 28, 28, 1) -> [... 3 layers ...] -> (?, 26, 26, 16)
In the example above, we specified network that expects images as an input. Each image will have height and width equal to 28x28 and we expect that each image will have only one channel.
It’s also fine to avoid specifying some of the dimension when value is unknown in advance. Unknown dimensions can be specified with value None.
>>> Input((None, None, 3)) >> Convolution((3, 3, 16)) >> Relu()
(?, ?, ?, 3) -> [... 3 layers ...] -> (?, ?, ?, 16)
>>>
>>> Input(None) >> Relu()
(?, ?) -> [... 2 layers ...] -> (?, ?)
Build networks from the code
For more complex networks, it’s possible to build them from the code. For example, we can dynamically specify depth of the network and build it in the loop.
>>> from neupy.layers import *
>>>
>>> network = Input(10)
>>> for size in (8, 6, 4, 2):
... network = network >> Sigmoid(size)
...
>>> network
(?, 10) -> [... 5 layers ...] -> (?, 2)
Code can be simplified by replacing network = network >> Sigmoid(size) with short expression - network >>= Sigmoid(size).
>>> network = Input(10)
>>> for size in (8, 6, 4, 2):
... network >>= Sigmoid(size)
...
>>> network
(?, 10) -> [... 5 layers ...] -> (?, 2)
Both examples are equivalent to the code below.
>>> network = join(
... Input(10),
... Sigmoid(8),
... Sigmoid(6),
... Sigmoid(4),
... Sigmoid(2),
... )
>>> network
(?, 10) -> [... 5 layers ...] -> (?, 2)
Mutlilayer Perceptron (MLP)
In this section, we are going to learn more about layers with activation function which are the most important building blocks for the MLP networks. Let’s consider the following example.
from neupy.layers import *
network = join(
Input(784),
Relu(500),
Relu(300),
Softmax(10),
)

You can see from the figure above that each layer with activation function defines dense connection. The NeuPy combines layer that applies linear transformation with non-linear activation function into one layer. It’s possible to break down this layer into two separate operations.
network = join(
Input(784),
Linear(500),
Relu(),
Linear(300),
Relu(),
Linear(10),
Softmax(),
)
Example above defines exactly the same architecture as before. We just split each layer with activation function into simple operations. Operation in the Relu(500) is the same as Linear(500) >> Relu().
Convolutional Neural Networks (CNN)
NeuPy supports Convolutional Neural Networks. Let’s consider the following example.
from neupy.layers import *
convnet = join(
Input((28, 28, 3)),
Convolution((3, 3, 32)),
Relu(),
Convolution((3, 3, 48)),
Relu(),
MaxPooling((2, 2)),
Reshape(),
Softmax(10),
)
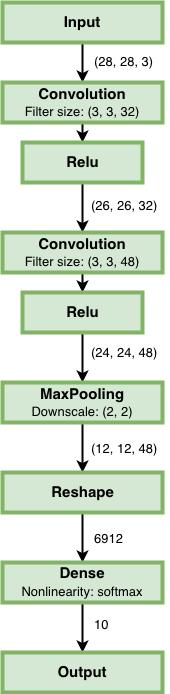
There are a few new layers that we are going to explore in more details.
Reshape
Reshape()
This layer does the same as the numpy.reshape function. The main different is that argument that defines new shape has default value. When shape is not specified explicitly, the Reshape layer converts input to 2D matrix.
>>> from neupy.layers import *
>>> Input((3, 10, 10)) >> Reshape()
(?, 3, 10, 10) -> [... 2 layers ...] -> (?, 300)
Also, we can specify expected output shape as a parameters for the Reshape layer.
>>> Input((3, 10, 10)) >> Reshape((3, 100))
(?, 3, 10, 10) -> [... 2 layers ...] -> (?, 3, 100)
Convolution
Convolution((3, 3, 32))
Each of the convolutional layers takes one mandatory argument that defines convolutional filter. Input argument contains three integers (number of rows, number of columns, number of filters). Information about the stack size was taken from the previous layer.
NeuPy supports only 2D convolution, but it’s trivial to make a 1D convolution. We can, for instance, set up width equal to 1 like in the following example.
>>> from neupy.layers import *
>>> join(
... Input((10, 30)),
... Reshape((10, 1, 30)),
... Convolution((3, 1, 16)),
... )
Convolutional layer has a few other attributes that you can modify. You can check the Convolutional layer’s documentation and find more information about its arguments.
Pooling
MaxPooling((2, 2))
Pooling layer has also one mandatory argument that defines a factor by which to downscale (vertical, horizontal). The (2, 2) value will halve the image in each dimension.
Pooling works only with 4D inputs, but you can use in case of 3D if you apply the same trick that we did for convolutional layer. You need to define one of the downscale factors equal to 1.
>>> from neupy.layers import *
>>> join(
... Input((10, 30)),
... Reshape((10, 1, 30)),
... MaxPooling((2, 1)),
... )
Parallel connections
Any connection between layers in NeuPy is a Directional Acyclic Graph (DAG). So far we’ve encountered only sequential connections which is just a simple case of DAG. In NeuPy, we are allowed to build much more complex relations between layers.
from neupy.layers import *
network = join(
Input((10, 10, 3)),
parallel([
Convolution((3, 3, 32)) >> Relu(),
MaxPooling((2, 2)),
], [
Convolution((7, 7, 16)) >> Relu(),
]),
Concatenate(),
Reshape(),
Softmax(10),
)
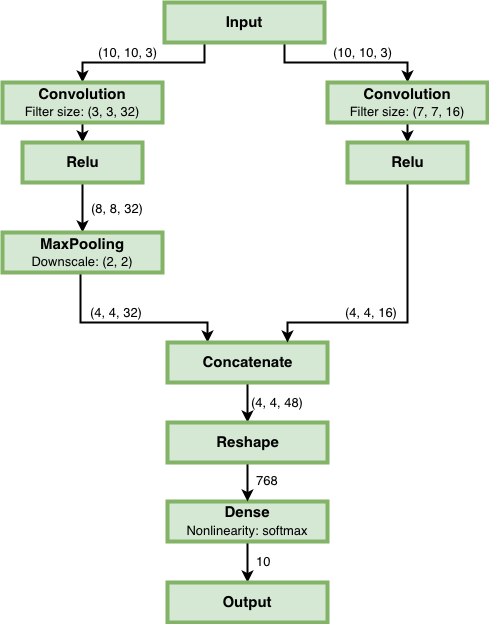
Also its possible to define the same graph relations between layers with inline operator.
>>> from neupy.layers import *
>>>
>>> input_layer = Input((10, 10, 3))
>>> left_branch = join(
... Convolution((3, 3, 32)) >> Relu(),
... MaxPooling((2, 2)),
... )
>>>
>>> right_branch = Convolution((7, 7, 16)) >> Relu()
>>>
>>> network = input_layer >> (left_branch | right_branch) >> Concatenate()
>>> network = network >> Reshape() >> Softmax()
Notice that we’ve used new operator. The | operator helps us to define parallel connections.
input_layer >> (left_branch | right_branch)
and many to one
(left_branch | right_branch) >> Concatenate()